Algorithms for Non-Negative Matrix Factorization on Noisy Data With Negative Values - Notes on Green et al. 2023

The paper “Algorithms for Non-Negative Matrix Factorization (NMF) on Noisy Data With Negative Values” addresses a common problem in applying NMF to real astrophysical data: noisy and negative data. NMF is a dimensionality reduction technique that has been used to analyse noisy data, especially in astronomy. My first reaction was to ask why we would want to apply a technique for non-negative data to negative data, but the reasoning is this: Astrophysical data, such as imaging and spectroscopy, deals with non-negative data. That is, the true signals are usually counts or count rates or fluxes, which by definition cannot be negative. However, the observed data can be negative due to noise. This can come from a variety of sources, such as instrument readout, calibration, or subtraction of an average from a noisy background. And the fluctuations that cause the negative values are still valid and important to consider.

There have been several ways to deal with this problem, such as weighting or using Monte Carlo analysis to determine the optimal solution. However, the problem is that these methods still do not take into account the negativity in the data matrix. One way to deal with this is to truncate the negative values to 0 or set them to a very small positive value. However, when looking at data with a low signal to noise ratio, the problem becomes apparent (note the offset from zero in the NMF Reconstruction (red)):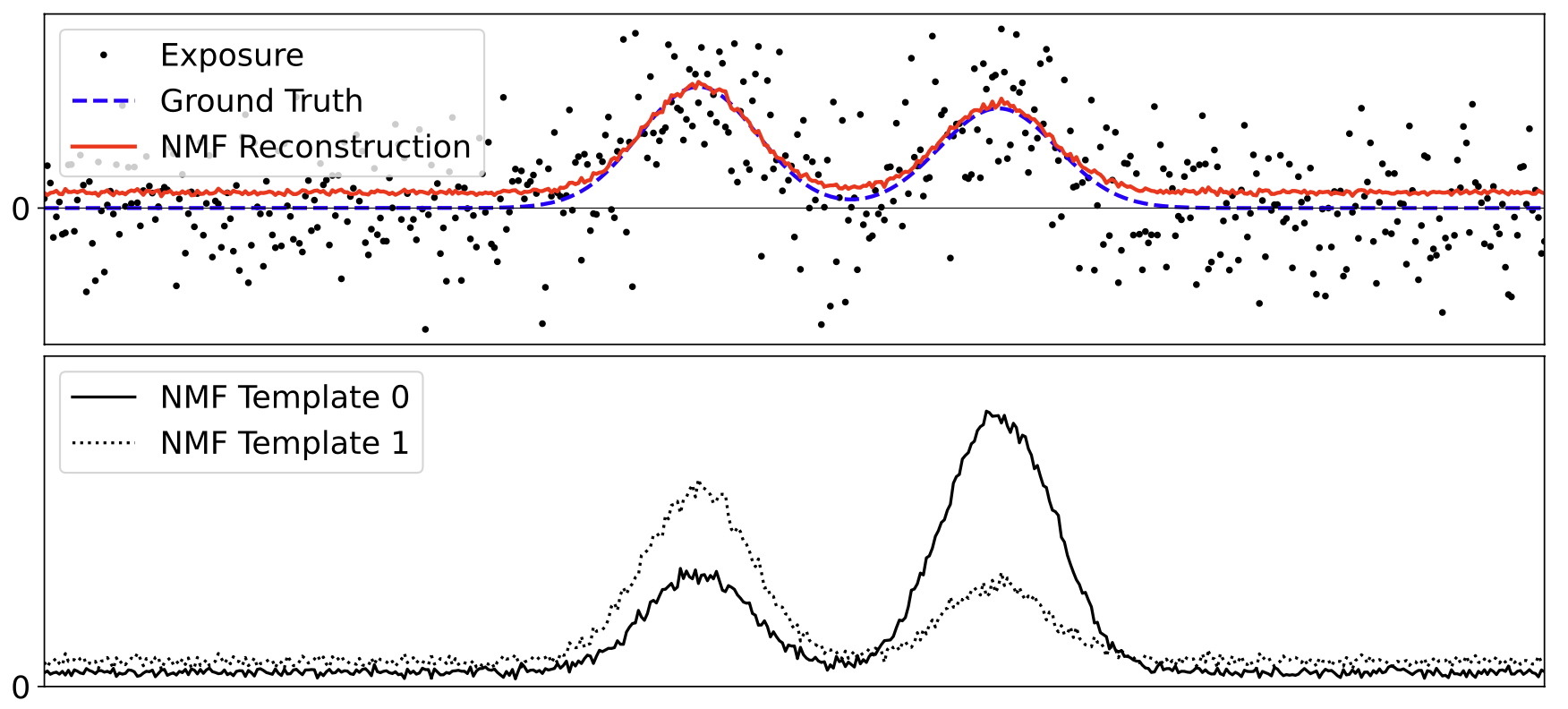

In this paper, they develop two new algorithms to correctly account for the negative data while still recovering strictly non-negative coefficients, and they call these algorithms Shift-NMF and Nearly-NMF:

• For Shift-NMF, the idea is to account for negative data by shifting and de-shifting the data.
• However, this makes convergence quite slow, so they introduced Nearly-NMF, which keeps the non-negative constraints on the output but removes them from the input data (I think it does this by introducing terms that go to zero for negative values).

The two new methods perform well on both a toy problem and simulated quasar data. First, a toy example, here you can see that the NMF “templates” (recovered components) go to zero and don’t have the problematic offset of the original NMF: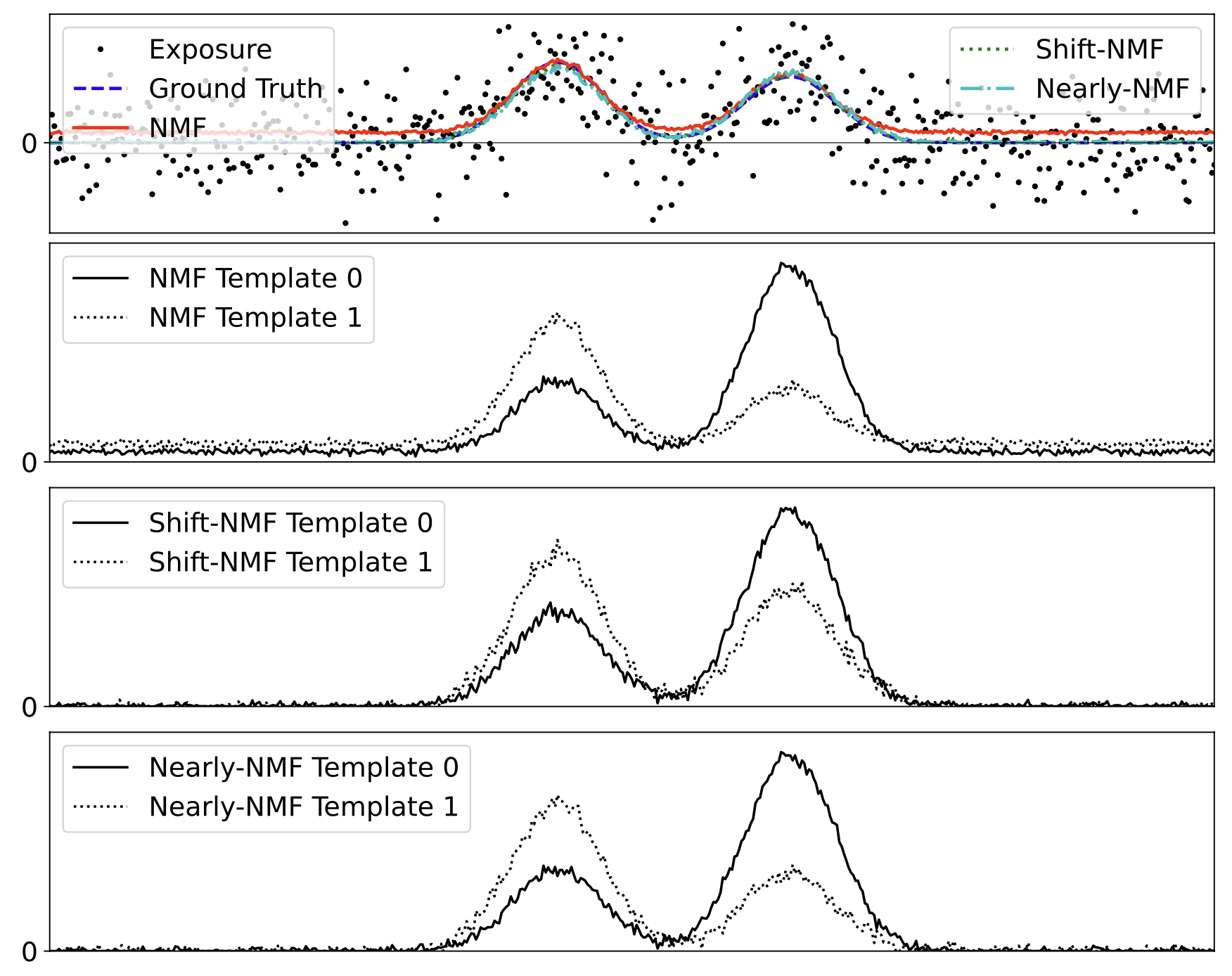

For the Quasar data, they simulated noiseless and noisy data for comparison, and as you can see from the chi-square values, these two results are almost identical: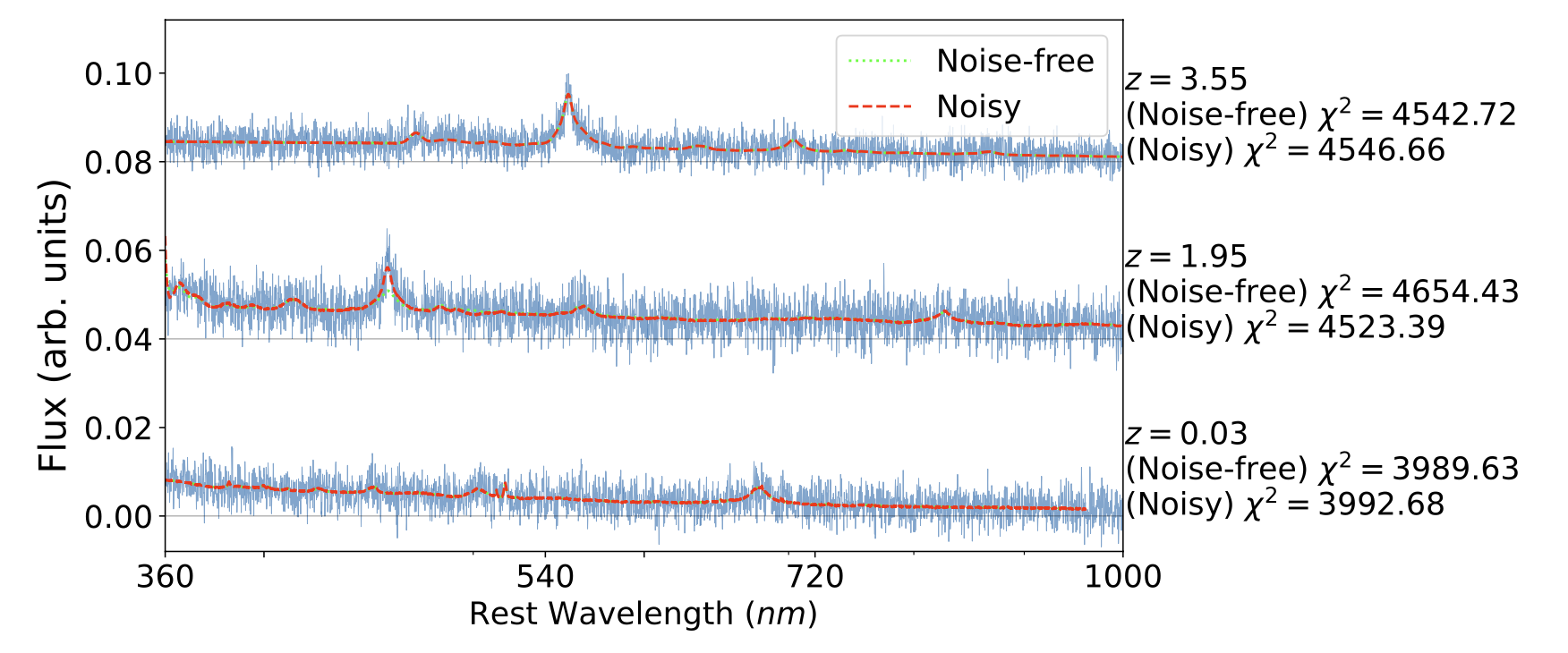

The algorithms are available on GitHub here.